푸리에 변환
푸리에 변환은 연속적인 시계열 데이터를 sin, cos 함수들과 같은 파형들의 합으로 나타내는 것으로 여러 개의 주파수 성분들로 분해하는 작업이다.
주로 신호 처리나 사운드, 이미지와 같은 데이터의 주파수 변환에 많이 사용한다.
그렇다면 어떻게 분해를 할 수 있는 것일까?
여기서는 이론적인 이해가 아닌 프로그래밍 구현측면에서 접근하도록 한다.
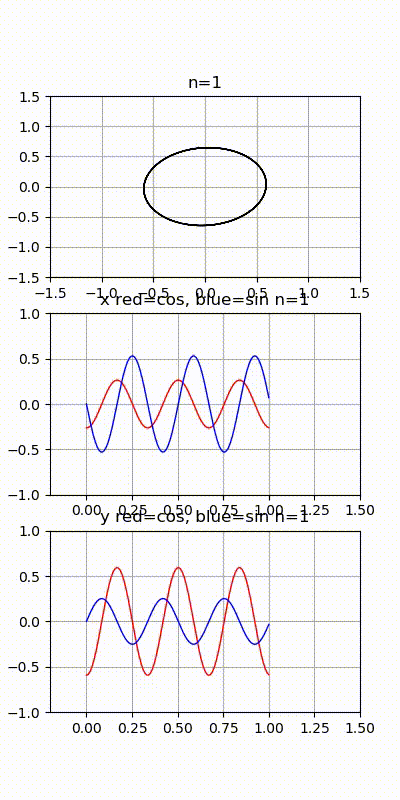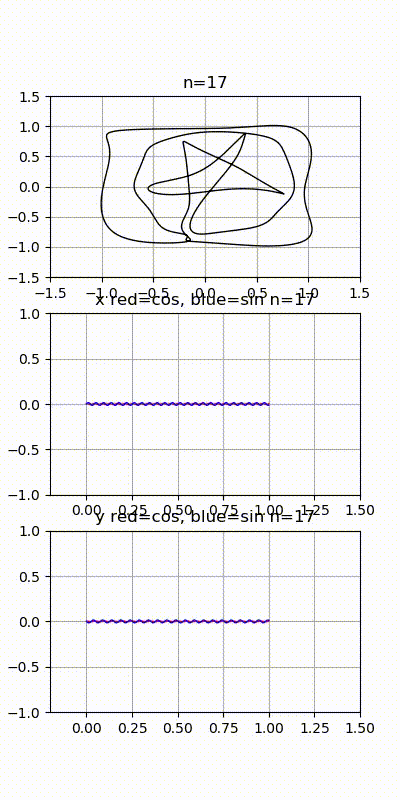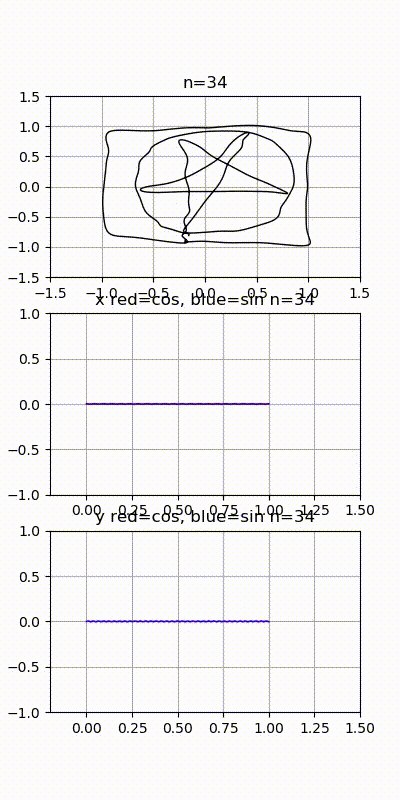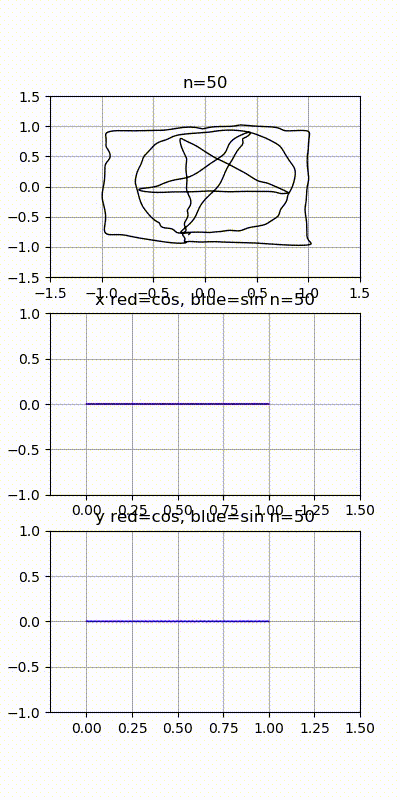
위 그림은 도형 이미지를 시간에 따른 x, y 좌표 리스트로 나누어 x, y 각각을 주파수 분해한 다음 분해된 주파수들을 하나씩 결합하여 그린 모양이다. 주파수를 하나씩 더 했을 때 점점 원본에 닮아가는 것을 확인할 수 있다.
노이즈가 섞인 원본 신호라면 주파수 분해 후 적절한 신호의 재결합을 통해 노이즈가 제거되는 효과도 나타날 수 있을 것이다.
도구
가장 쉽게 접근할 수 있는 것은 python의 numpy나 scipy 라이브러리로 쉽게 원하는 작업을 할 수 있다. cpp로 된 라이브러리도 google에서 검색하면 금방 찾을 수 있다.
해결하려는 문제
시계열 데이터를 주파수 성분으로 분해하고 분해된 수치 정보만으로 원본을 복구하는 작업을 수행하고자 한다.
알 수 없는 시그널
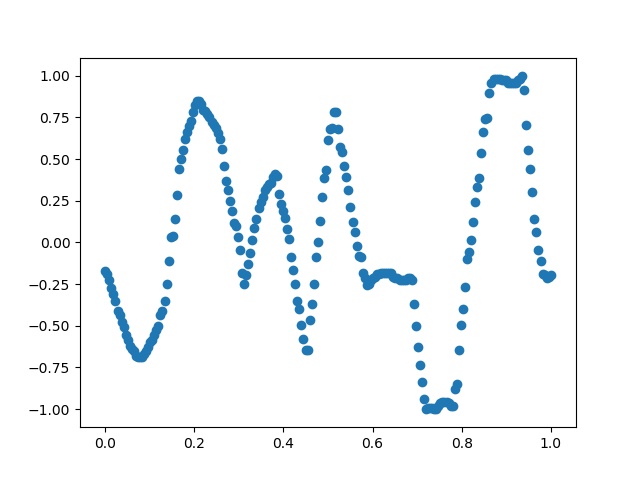
시간값과 신호크기만 있는 시계열 데이터가 있다고 하자.
'''
foutier transform
'''
import numpy as np
import matplotlib.pyplot as plt
txlist = [(0.0, -0.1729957805907173), (0.0045871559633027525, -0.189873417721519), (0.009174311926605505, -0.2236286919831224), (0.013761467889908258, -0.2742616033755274), (0.01834862385321101, -0.3080168776371308), (0.022935779816513763, -0.3502109704641351), (0.027522935779816515, -0.4092827004219409), (0.03211009174311927, -0.4345991561181435), (0.03669724770642202, -0.47679324894514763), (0.04128440366972477, -0.510548523206751), (0.045871559633027525, -0.5527426160337553), (0.05045871559633028, -0.5864978902953586), (0.05504587155963303, -0.620253164556962), (0.05963302752293578, -0.6371308016877637), (0.06422018348623854, -0.6540084388185654), (0.06880733944954129, -0.6793248945147679), (0.07339449541284404, -0.6877637130801688), (0.0779816513761468, -0.6877637130801688), (0.08256880733944955, -0.6877637130801688), (0.0871559633027523, -0.6708860759493671), (0.09174311926605505, -0.6540084388185654), (0.0963302752293578, -0.6286919831223629), (0.10091743119266056, -0.5949367088607596), (0.10550458715596331, -0.5864978902953586), (0.11009174311926606, -0.5527426160337553), (0.11467889908256881, -0.5274261603375527), (0.11926605504587157, -0.5021097046413502), (0.12385321100917432, -0.4345991561181435), (0.12844036697247707, -0.4092827004219409), (0.13302752293577982, -0.3502109704641351), (0.13761467889908258, -0.24894514767932485), (0.14220183486238533, -0.11392405063291144), (0.14678899082568808, 0.029535864978903037), (0.15137614678899083, 0.03797468354430378), (0.1559633027522936, 0.139240506329114), (0.16055045871559634, 0.28270042194092837), (0.1651376146788991, 0.4430379746835442), (0.16972477064220184, 0.5021097046413503), (0.1743119266055046, 0.5527426160337552), (0.17889908256880735, 0.620253164556962), (0.1834862385321101, 0.6624472573839661), (0.18807339449541285, 0.6962025316455696), (0.1926605504587156, 0.729957805907173), (0.19724770642201836, 0.7805907172995781), (0.2018348623853211, 0.8227848101265822), (0.20642201834862386, 0.8481012658227849), (0.21100917431192662, 0.8481012658227849), (0.21559633027522937, 0.8312236286919832), (0.22018348623853212, 0.7974683544303798), (0.22477064220183487, 0.7890295358649788), (0.22935779816513763, 0.7721518987341771), (0.23394495412844038, 0.7552742616033756), (0.23853211009174313, 0.7215189873417722), (0.24311926605504589, 0.7046413502109705), (0.24770642201834864, 0.6877637130801688), (0.25229357798165136, 0.6540084388185654), (0.25688073394495414, 0.620253164556962), (0.26146788990825687, 0.5611814345991561), (0.26605504587155965, 0.4599156118143459), (0.2706422018348624, 0.36708860759493667), (0.27522935779816515, 0.31645569620253156), (0.2798165137614679, 0.24894514767932496), (0.28440366972477066, 0.1898734177215189), (0.2889908256880734, 0.11392405063291133), (0.29357798165137616, 0.09704641350210963), (0.2981651376146789, 0.029535864978903037), (0.30275229357798167, -0.04641350210970463), (0.3073394495412844, -0.18143459915611815), (0.3119266055045872, -0.24894514767932485), (0.3165137614678899, -0.19831223628691985), (0.3211009174311927, -0.13080168776371304), (0.3256880733944954, -0.06329113924050633), (0.3302752293577982, 0.012658227848101333), (0.3348623853211009, 0.08860759493670889), (0.3394495412844037, 0.139240506329114), (0.3440366972477064, 0.2067510548523206), (0.3486238532110092, 0.240506329113924), (0.3532110091743119, 0.2742616033755274), (0.3577981651376147, 0.31645569620253156), (0.3623853211009174, 0.33333333333333326), (0.3669724770642202, 0.35021097046413496), (0.37155963302752293, 0.3586497890295359), (0.3761467889908257, 0.39240506329113933), (0.38073394495412843, 0.40928270042194104), (0.3853211009174312, 0.4008438818565401), (0.38990825688073394, 0.2911392405063291), (0.3944954128440367, 0.23206751054852326), (0.39908256880733944, 0.1898734177215189), (0.4036697247706422, 0.14767932489451474), (0.40825688073394495, 0.08016877637130793), (0.41284403669724773, 0.021097046413502074), (0.41743119266055045, -0.08860759493670889), (0.42201834862385323, -0.16455696202531644), (0.42660550458715596, -0.24894514767932485), (0.43119266055045874, -0.3502109704641351), (0.43577981651376146, -0.4008438818565401), (0.44036697247706424, -0.49367088607594933), (0.44495412844036697, -0.5780590717299579), (0.44954128440366975, -0.6455696202531646), (0.4541284403669725, -0.6455696202531646), (0.45871559633027525, -0.4683544303797469), (0.463302752293578, -0.36708860759493667), (0.46788990825688076, -0.24894514767932485), (0.4724770642201835, -0.08860759493670889), (0.47706422018348627, 0.00421940928270037), (0.481651376146789, 0.13080168776371304), (0.48623853211009177, 0.2742616033755274), (0.4908256880733945, 0.38396624472573837), (0.4954128440366973, 0.4345991561181435), (0.5, 0.6118143459915613), (0.5045871559633027, 0.6793248945147679), (0.5091743119266054, 0.6877637130801688), (0.5137614678899083, 0.7805907172995781), (0.518348623853211, 0.7805907172995781), (0.5229357798165137, 0.6793248945147679), (0.5275229357798165, 0.5696202531645569), (0.5321100917431193, 0.5443037974683544), (0.536697247706422, 0.4599156118143459), (0.5412844036697247, 0.39240506329113933), (0.5458715596330275, 0.31645569620253156), (0.5504587155963303, 0.21518987341772156), (0.555045871559633, 0.1223628691983123), (0.5596330275229358, 0.06329113924050622), (0.5642201834862385, -0.021097046413502074), (0.5688073394495413, -0.08016877637130804), (0.573394495412844, -0.08860759493670889), (0.5779816513761468, -0.18143459915611815), (0.5825688073394495, -0.21518987341772156), (0.5871559633027523, -0.2573839662447257), (0.591743119266055, -0.24894514767932485), (0.5963302752293578, -0.2236286919831224), (0.6009174311926605, -0.21518987341772156), (0.6055045871559633, -0.2067510548523207), (0.6100917431192661, -0.189873417721519), (0.6146788990825688, -0.189873417721519), (0.6192660550458715, -0.18143459915611815), (0.6238532110091743, -0.18143459915611815), (0.6284403669724771, -0.18143459915611815), (0.6330275229357798, -0.18143459915611815), (0.6376146788990825, -0.18143459915611815), (0.6422018348623854, -0.18143459915611815), (0.6467889908256881, -0.2067510548523207), (0.6513761467889908, -0.21518987341772156), (0.6559633027522935, -0.21518987341772156), (0.6605504587155964, -0.2236286919831224), (0.6651376146788991, -0.2236286919831224), (0.6697247706422018, -0.2236286919831224), (0.6743119266055045, -0.2236286919831224), (0.6788990825688074, -0.21518987341772156), (0.6834862385321101, -0.21518987341772156), (0.6880733944954128, -0.2236286919831224), (0.6926605504587156, -0.36708860759493667), (0.6972477064220184, -0.5021097046413502), (0.7018348623853211, -0.6286919831223629), (0.7064220183486238, -0.7383966244725738), (0.7110091743119266, -0.8396624472573839), (0.7155963302752294, -0.9409282700421941), (0.7201834862385321, -1.0), (0.7247706422018348, -0.9915611814345991), (0.7293577981651376, -0.9915611814345991), (0.7339449541284404, -0.9915611814345991), (0.7385321100917431, -1.0), (0.7431192660550459, -1.0), (0.7477064220183486, -0.9831223628691983), (0.7522935779816514, -0.9662447257383966), (0.7568807339449541, -0.9578059071729957), (0.7614678899082569, -0.9578059071729957), (0.7660550458715596, -0.9578059071729957), (0.7706422018348624, -0.9662447257383966), (0.7752293577981652, -0.9831223628691983), (0.7798165137614679, -0.9831223628691983), (0.7844036697247706, -0.8818565400843882), (0.7889908256880734, -0.8481012658227848), (0.7935779816513762, -0.6455696202531646), (0.7981651376146789, -0.49367088607594933), (0.8027522935779816, -0.4008438818565401), (0.8073394495412844, -0.26582278481012656), (0.8119266055045872, -0.09704641350210974), (0.8165137614678899, -0.05485232067510548), (0.8211009174311926, 0.012658227848101333), (0.8256880733944955, 0.1223628691983123), (0.8302752293577982, 0.240506329113924), (0.8348623853211009, 0.33333333333333326), (0.8394495412844036, 0.38396624472573837), (0.8440366972477065, 0.5358649789029535), (0.8486238532110092, 0.6624472573839661), (0.8532110091743119, 0.7383966244725739), (0.8577981651376146, 0.7468354430379747), (0.8623853211009175, 0.8987341772151898), (0.8669724770642202, 0.9578059071729959), (0.8715596330275229, 0.9831223628691983), (0.8761467889908257, 0.9831223628691983), (0.8807339449541285, 0.9831223628691983), (0.8853211009174312, 0.9831223628691983), (0.8899082568807339, 0.9746835443037976), (0.8944954128440367, 0.9746835443037976), (0.8990825688073395, 0.9746835443037976), (0.9036697247706422, 0.9578059071729959), (0.908256880733945, 0.9578059071729959), (0.9128440366972477, 0.9578059071729959), (0.9174311926605505, 0.9578059071729959), (0.9220183486238532, 0.9578059071729959), (0.926605504587156, 0.9746835443037976), (0.9311926605504587, 0.9831223628691983), (0.9357798165137615, 1.0), (0.9403669724770642, 0.9156118143459915), (0.944954128440367, 0.7046413502109705), (0.9495412844036697, 0.5527426160337552), (0.9541284403669725, 0.4430379746835442), (0.9587155963302753, 0.29957805907172985), (0.963302752293578, 0.139240506329114), (0.9678899082568807, 0.06329113924050622), (0.9724770642201835, -0.04641350210970463), (0.9770642201834863, -0.11392405063291144), (0.981651376146789, -0.189873417721519), (0.9862385321100917, -0.19831223628691985), (0.9908256880733946, -0.21518987341772156), (0.9954128440366973, -0.2067510548523207), (1.0, -0.19831223628691985)]
txlist = np.asarray(txlist)
plt.figure()
plt.scatter(txlist[:,0], txlist[:,1])
plt.savefig('fft02.jpg')
plt.show()
위와 같은 그래프로 표현되는 원본 시그널이 있을 때, 수집된 샘플 데이터의 수가 부족할 수도 있다. 이 때는 보간법으로 점들 사이의 데이터들을 추정하여 채울 수 있다.
일정한 시간간격으로 추정된 위치값을 보간법으로 구해 데이터 수를 확장해 보자.
보간법
우리가 필요한 샘플링 주기는 최대 주파수 설정에 따른다.
최대 500Hz까지를 검사하여 성분 분석을 하려면 그 두배인 1000Hz를 maxfreq로 설정한다.
(나중에 나오지만 주파수 스펙트럼을 그려보면 중앙을 기준으로 좌우 대칭으로 나온다. 따라서 최대 주파수 *2를 해준다.)
1000Hz를 maxfreq로 잡으면 샘플링 주기는 1/1000 sec로 한다.
일정한 시간간격 (1ms)마다의 신호크기를 추정해 다시 그려보자.
from scipy.interpolate import splrep, splev
spl = splrep(txlist[:,0], txlist[:,1])
fs = 1000
dt = 1/fs
spl = splrep(txlist[:,0], txlist[:,1])
newt = np.arange(0, 1, dt)
newx = splev(newt, spl)
print(newt)
print(newx)
if True:
plt.figure()
plt.scatter(newt, newx)
plt.savefig('fft02_2.jpg')
plt.show()
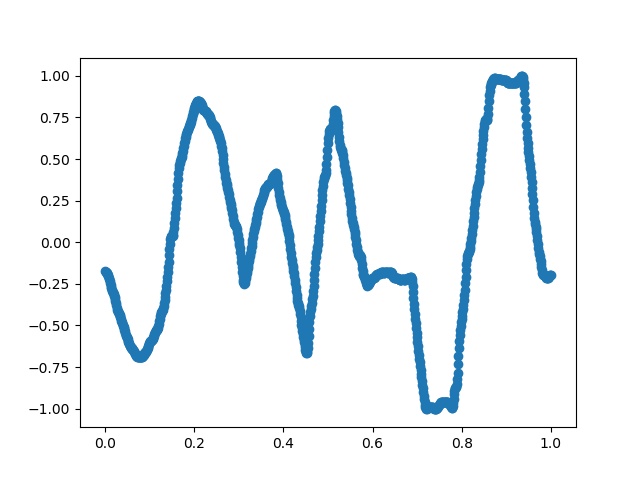
FFT
위 신호를 분해해 보자.
먼저 주파수 스펙트럼을 구해서 어떤 주파수를 사용해야 하는지를 분석한다. 스펙트럼 그래프에서 높은 값을 가진 성분의 주파수를 선택하면 된다.
nfft = len(newt)
print('nfft = ', nfft)
df = fs/nfft
k = np.arange(nfft)
f = k*df
nfft_half = math.trunc(nfft/2)
f0 = f[range(nfft_half)]
y = np.fft.fft(newx)/nfft * 2
y0 = y[range(nfft_half)]
amp = abs(y0)
if True:
plt.figure()
plt.plot(f0, amp)
plt.savefig('fft02_3.jpg')
plt.show()
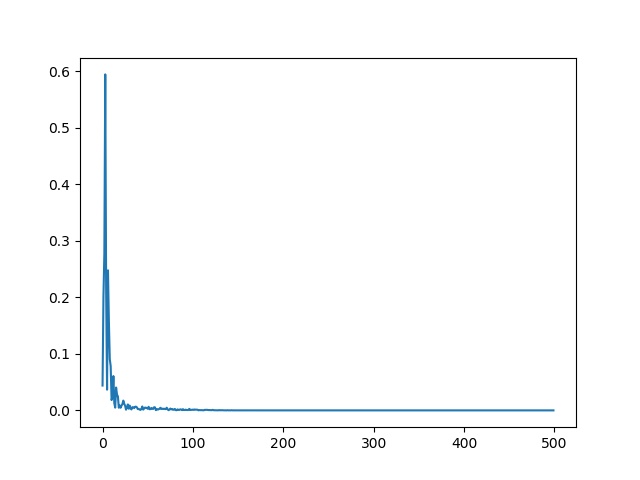
위 그래프의 가로축은 주파수이고 세로축은 신호 강도이다.
작은 값을 버리고 강도가 센 주파수만 선별하면 된다.
top N개를 설정해서 몇 개만 할 수 도 있지만, 몇 개가 최적인지 알 수 없기에 사분위수의 극단점을 이용해 보았다. (데이터 분포의 25%~75%범위의 끝에서 해당 크기의 1.5배 이상 떨어진 데이터)
굳이 이렇게까지 할 필요는 없고 특정 개수로 (예를 들면 10개로) 설정해도 된다.
ampsort = np.sort(amp)
q1, q3 = np.percentile(ampsort, [25, 75])
iqr = q3-q1
upper_bound = q3+1.5*iqr
print('q1=',q1, 'q3=',q3, 'upper_bound=', upper_bound)
outer = ampsort[ampsort>upper_bound]
print('outer cnt=', len(outer))
topn = len(outer)
print(outer)
1000 개중에 특이하게 높은 값 101개를 찾았다.
nfft = 1000
q1= 2.7017249783348636e-05 q3= 0.00031241349163501486 upper_bound= 0.0007405078544125142
outer cnt= 101
[0.00081545 0.00085501 0.00086458 0.00090005 0.00090194 0.00091519
0.00091733 0.00093784 0.00096499 0.00097396 0.00099638 0.00104299
0.00107283 0.00126076 0.00126265 0.00127681 0.00129231 0.00131356....]
상위 101개의 주파수를 찾는다.
idxy = np.argsort(-amp)
for i in range(topn):
print('freq=', f0[idxy[i]], 'amp=', y[idxy[i]])
마지막으로 주파수만으로 원본을 추정해 그려본다.
newy = np.zeros((nfft,))
arfreq = []
arcoec = []
arcoes = []
for i in range(topn):
freq = f0[idxy[i]]
yx = y[idxy[i]]
coec = yx.real
coes = yx.imag * -1
print('freq=', freq, 'coec=', coec, ' coes', coes)
newy += coec * np.cos(2 * np.pi * freq * newt) + coes * np.sin(2 * np.pi * freq * newt)
arfreq.append(freq)
arcoec.append(coec)
arcoes.append(coes)
plt.figure()
plt.plot(txlist[:,0], txlist[:,1], c='r', label='orginal')
plt.plot(newt, newy, c='b', label='fft')
plt.legend()
plt.savefig('fft02_4.jpg')
plt.show()
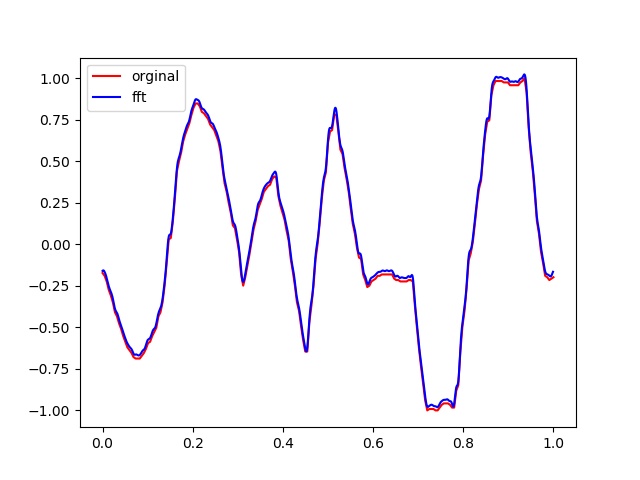
거의 복원된 모습을 확인할 수 있다.
주성분 주파수를 하나씩 추가하여 변화하는 모습을 확인해 보자.
plt.figure()
plti = 0
ncnt = 15
newy = np.zeros((nfft,))
for i in range(ncnt+1):
freq = f0[idxy[i]]
yx = y[idxy[i]]
coec = yx.real
coes = yx.imag * -1
print('freq=', freq, 'coec=', coec, ' coes', coes)
newy += coec * np.cos(2 * np.pi * freq * newt) + coes * np.sin(2 * np.pi * freq * newt)
plti+=1
plt.subplot(4,4, plti)
plt.title("N={}".format(i+1))
plt.plot(newt, newy)
plt.savefig('fft02_5.jpg')
plt.show()
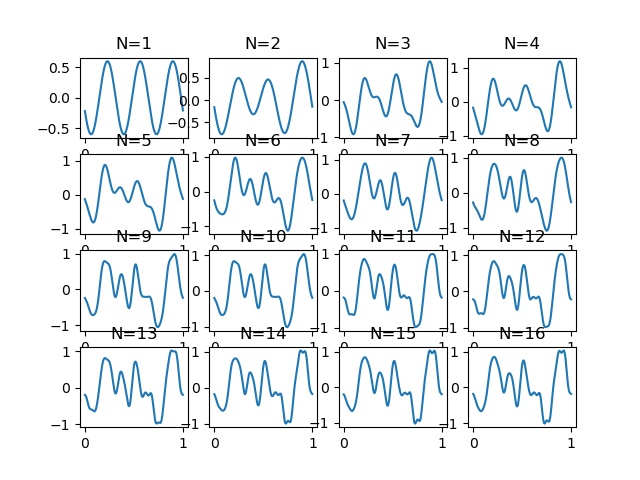
주파수를 추가할 때 마다 점점 원본의 모습으로 바뀌어진다.
Authors: crazyj7@gmail.com
Written with StackEdit.








