Crawling 2 WebDriver

브라우저로 볼때는 분명 데이터가 있는데, 크롤링으로 HTML을 가져와서 보면 없는 경우가 있다.
이것은 브라우저에는 JS를 구동기능이 포함되어 HTML 문서가 동적으로 변화하기 때문에 단순하게 네트웍으로 HTML 문서를 받은 것과 항상 일치한다는 보장이 없기 때문이다
따라서 브라우저처럼 작동하여 변화된 HTML을 만들면 원하는 정보를 얻을 수 있는데 이것이 web driver이다.

구글 크롬 브라우저의 경우 이러한 것을 제공한다.
파이썬에서는 selenium 패키지를 설치하고, 운영체제에는 ChromeDriver를 설치해야 한다.
중요한 것은 현재 크롬브라우저의 버전과 ChromeDriver의 버전이 일치해야 한다!!!
버전이 다르다면 작동하지 않을 것이다.

https://sites.google.com/a/chromium.org/chromedriver/downloads

여기에서 자신의 크롬브라우저와 같은 버전의 드라이버를 받는다. 드라이버는 실행파일인데, PATH에 연결된 경로에 실행파일을 복사하면 준비가 다 된것이다.

전에 실패한 실시간 기사 조회

전에 코드에서 html 을 urllib으로 가져오지 말고 web driver를 구동하여 가져와서 파싱해 보자.

from selenium import webdriver
from bs4 import BeautifulSoup

url = 'https://m.media.daum.net/m/media/economic'

options = webdriver.ChromeOptions()
options.add_argument('headless')
browser = webdriver.Chrome(chrome_options=options)
browser.implicitly_wait(3)

browser.get(url)
html = browser.page_source
soup = BeautifulSoup(html, 'html.parser')

subnews = soup.find("div", "section_sub")
realnews = subnews.find("div", "box_realtime")
print(realnews)

browser.quit()

output

<div class="box_g box_realtime">
<h3 class="tit_g">실시간 주요 경제 뉴스</h3>
<ul category="economic" class="list_thumb">
<li>
<a class="link_news #MAIN_NEWS#article @1" href="http://v.media.daum.net/v/20191023201603468?f=m">
<div class="wrap_thumb">
<img alt="삼성물산 '1조6천억 분식회계' 적발..수천억 손실이 순익 둔갑" class="thumb_g" height="68" src="//t1.daumcdn.net/thumb/F240x180ht.u/?fname=https%3A%2F%2Ft1.daumcdn.net%2Fnews%2F201910%2F23%2Fhani%2F20191023201603606uvoz.jpg"/>
</div>
<div class="cont_thumb">
<strong class="tit_thumb">
<span class="txt_g">삼성물산 '1조6천억 분식회계' 적발..수천억 손실이 순익 둔갑</span>
<span class="txt_cp">5분전</span>
</strong>
</div>
</a>
</li>
<li>
<a class="link_news #MAIN_NEWS#article @2" href="http://v.media.daum.net/v/20191023191757086?f=m">
<div class="wrap_thumb">
<img alt='野, 기재부에 "민부론 검토자료 내놔라"..與 "제출 의무 없어"' class="thumb_g" height="68" src="//t1.daumcdn.net/thumb/F240x180ht.u/?fname=https%3A%2F%2Ft1.daumcdn.net%2Fnews%2F201910%2F23%2Fnewsis%2F20191023191757773esif.jpg"/>
</div>
<div class="cont_thumb">
<strong class="tit_thumb">
<span class="txt_g">野, 기재부에 "민부론 검토자료 내놔라"..與 "제출 의무 없어"</span>
<span class="txt_cp">1시간전</span>

전에는 ul 태그 내부가 비었었는데 이제 내용을 가져올 수 있게 되었다.
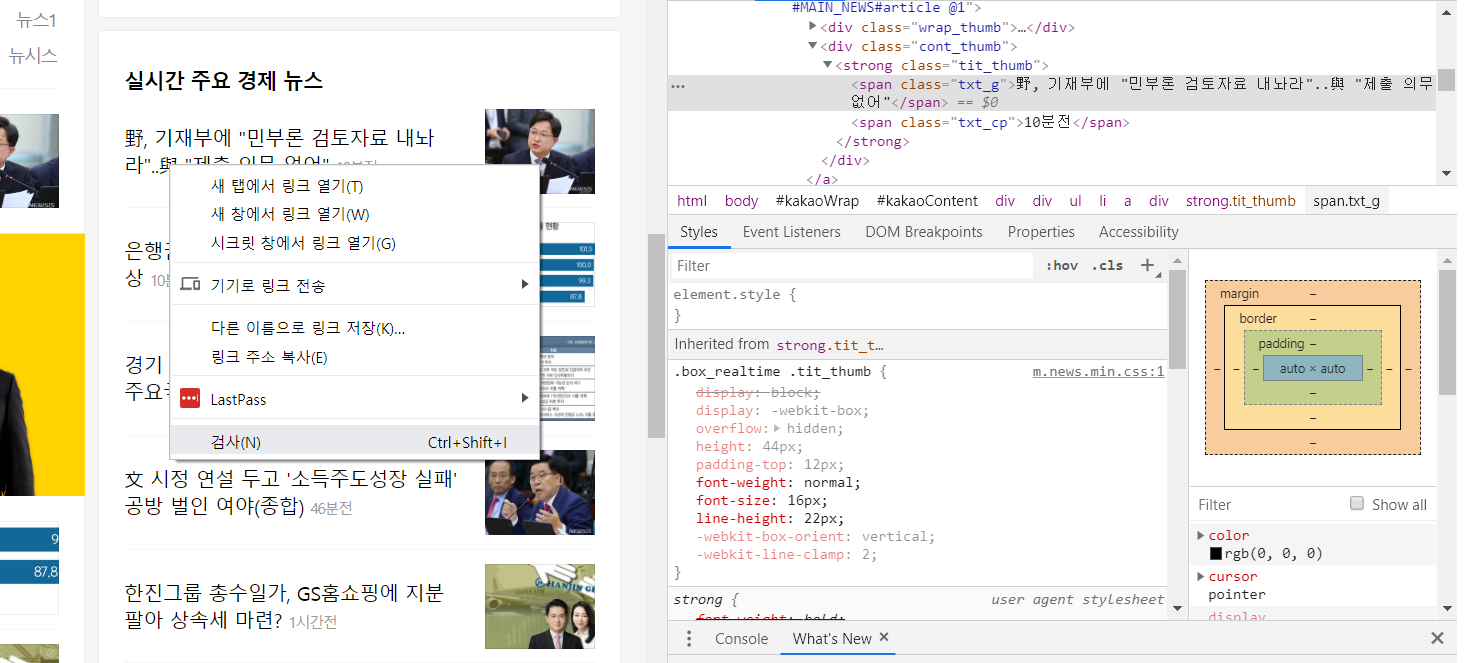
코드를 정리하여 기사 제목만 가져와보자. 이것도 좀 더 쉽게 하려면 F12키로 개발자모드로 간 다음 추출할 부분에 대해 selector 값을 쉽게 가져올 수 있다.

selector를 적당히 수정하면 목록을 쉽게 추출할 수있다.

# news = soup.select('#kakaoContent > div.section_sub > div.box_g.box_realtime > ul > li:nth-child(1) > a > div.cont_thumb > strong > span.txt_g')
news = soup.select('#kakaoContent > div.section_sub > div.box_g.box_realtime > ul > li > a > div.cont_thumb > strong > span.txt_g')
for item in news:
    print(item.text)

output

삼성물산 '1조6천억 분식회계' 적발..수천억 손실이 순익 둔갑
野, 기재부에 "민부론 검토자료 내놔라"..與 "제출 의무 없어"
은행권 "예대율 낮춰라".. 예금 확보 비상
경기 하강기 커지는 재정 역할.."세계 주요국도 확장 정책"
文 시정 연설 두고 '소득주도성장 실패' 공방 벌인 여야(종합)
한진그룹 총수일가, GS홈쇼핑에 지분 팔아 상속세 마련?
홍남기 "법인세 인하 투자증가로 연결 안 돼..신중한 입장"
김영진, 기재위 국감서 '황교안 계엄령 개입' 의혹 언급..野 반발
[단독]에어부산, 괌에서 '기체결함'으로 긴급 회항..13시간 지연 출항
[단독]정부 '직무급 도입-임금체계 개편' 병합 논의

전에 단순한 방식으로 안되는 작업이 이제 원하는 부분을 깔끔하게 추출하였다.

추가로…

아래는 만약 같은 페이지내에서 뭔가를 클릭해야 내용이 더 보여서 그 내용도 추출하기 위한 작업이다.

다음 실시간 검색어 조회

모바일용 웹 주소를 이용하였다. 일반 PC용 주소로 사용하면 데이터가 많아서 느릴 수 있으니 텍스트 위주의 페이지로 접근하는 것이 더 용이하다.
중간에 보면 실시간 검색어 목록이 다 나오도록 확장 버튼을 클릭하는 것을 추가하였다.

from selenium import webdriver
from bs4 import BeautifulSoup

def getTop10Daum():
    url = "https://m.daum.net"

    # browser = webdriver.PhantomJS()
    # browser.implicitly_wait(3)

    options = webdriver.ChromeOptions()
    options.add_argument('headless')
    # browser = webdriver.Chrome(options=options)
    # browser = webdriver.Chrome()
    browser = webdriver.Chrome(chrome_options=options)
    browser.implicitly_wait(3)

    browser.get(url)
    browser.save_screenshot("web1.png")

    # mAside > div.head_issue > div.roll_issue.\#searchrank\#rolling > strong > a

    # browser.find_element_by_xpath('//*[@id="mAside"]/div[1]/div[1]/strong/a').click()
    browser.find_element_by_css_selector('div.roll_issue.\#searchrank\#rolling > strong > a').click()
    browser.save_screenshot("web2.png")

    html = browser.page_source
    soup = BeautifulSoup(html, 'html.parser')
    # print(soup)
    notices = soup.select('div.realtime_layer div.panel')

    resultlist = []

    for n in notices:
        # print ('aria-hidden-', n['aria-hidden'])
        if n['aria-hidden']=='false':
            lis = n.select('li')
            for l in lis:
                result = dict()
                result['rank'] = l.select_one('.num_issue').text
                result['title']= l.select_one('.txt_issue').text
                result['url'] = l.a['href']
                # print(l.select_one('.num_issue').text)
                # print(l.select_one('.txt_issue').text)
                # print('href=',l.a['href'])
                resultlist.append(result)
    browser.quit()

    # print(resultlist)
    return resultlist


if __name__ == '__main__':
    items = getTop10Daum()
    for it in items:
        print(it['rank'], it['title'], it['url'])

output

1 서효림 https://m.search.daum.net/search?w=tot&q=%EC%84%9C%ED%9A%A8%EB%A6%BC&DA=ATG&nil_mtopsearch=issuekwd&logical=issue&pin=issue
2 이다희 https://m.search.daum.net/search?w=tot&q=%EC%9D%B4%EB%8B%A4%ED%9D%AC&DA=ATG&nil_mtopsearch=issuekwd&logical=issue&pin=issue
3 김칠준 변호사 https://m.search.daum.net/search?w=tot&q=%EA%B9%80%EC%B9%A0%EC%A4%80+%EB%B3%80%ED%98%B8%EC%82%AC&DA=ATG&nil_mtopsearch=issuekwd&logical=issue&pin=issue
4 정경심 교수 https://m.search.daum.net/search?w=tot&q=%EC%A0%95%EA%B2%BD%EC%8B%AC+%EA%B5%90%EC%88%98&DA=ATG&nil_mtopsearch=issuekwd&logical=issue&pin=issue
5 송성문 https://m.search.daum.net/search?w=tot&q=%EC%86%A1%EC%84%B1%EB%AC%B8&DA=ATG&nil_mtopsearch=issuekwd&logical=issue&pin=issue
6 김준기 https://m.search.daum.net/search?w=tot&q=%EA%B9%80%EC%A4%80%EA%B8%B0&DA=ATG&nil_mtopsearch=issuekwd&logical=issue&pin=issue
7 오재일 https://m.search.daum.net/search?w=tot&q=%EC%98%A4%EC%9E%AC%EC%9D%BC&DA=ATG&nil_mtopsearch=issuekwd&logical=issue&pin=issue
8 김수미 아들 https://m.search.daum.net/search?w=tot&q=%EA%B9%80%EC%88%98%EB%AF%B8+%EC%95%84%EB%93%A4&DA=ATG&nil_mtopsearch=issuekwd&logical=issue&pin=issue
9 인헌고등학교 https://m.search.daum.net/search?w=tot&q=%EC%9D%B8%ED%97%8C%EA%B3%A0%EB%93%B1%ED%95%99%EA%B5%90&DA=ATG&nil_mtopsearch=issuekwd&logical=issue&pin=issue
10 이승호 https://m.search.daum.net/search?w=tot&q=%EC%9D%B4%EC%8A%B9%ED%98%B8&DA=ATG&nil_mtopsearch=issuekwd&logical=issue&pin=issue

Author: crazyj7@gmail.com

91. $\int \frac{x}{1 + x^4} dx$

$\begin{aligned} &\int \frac{x}{1 + x^4} dx \\ &u=x^2, du=2xdx\\ &=\frac{1}{2}\int \frac{1}{1+u^2}du=\frac{1}{2}arctan(u)\\ &=\frac{1}{2}arctan(x^2)+C\\ \end{aligned}$

92. $\int e^{\sqrt x} dx$

$\begin{aligned} &\int e^{\sqrt x} dx \\ & u=\sqrt x , du=\frac{1}{2\sqrt x} dx\\ &\int e^u 2udu=2\int ue^udu=2( ue^u-e^u )\\ &=2e^{\sqrt x}(\sqrt x -1 )+C \end{aligned}$

93. $\int \frac{1}{csc(x)^3} dx$

$\begin{aligned} &\int \frac{1}{csc(x)^3} dx \\ &=\int sin^3(x) dx=\int sin(x)(1-cos^2x)dx\\ &=\int sin(x)dx-\int sin(x)cos^2xdx\\ &(u=cos(x), du=-sin(x)dx)\\ &=-cos(x)+\int u^2du=-cos(x)+\frac{1}{3}u^3+C\\ &=-cos(x)+\frac{1}{3}cos^3x+C \end{aligned}$

94. $\int \frac{arcsin x}{\sqrt{1 - x^2}}dx$

$\begin{aligned} &\int \frac{arcsin x}{\sqrt{1 - x^2}} \\ &( \frac{1}{\sqrt{1-x^2}} -int-> arcsin(x) )\\ &u=arcsin(x), du=\frac{1}{\sqrt{1-x^2}}dx\\ &=\int u du = \frac{1}{2} u^2=\frac{(sin^{-1}x)^2}{2}+C \end{aligned}$

95. $\int \sqrt{1 + sin(2x)} dx$

$\begin{aligned} &\int \sqrt{1 + sin(2x)} dx \\ &u=sin(2x) , du=2cos(2x)dx\\ &=\int \sqrt {1+u} \frac{1}{2cos(2x)}du =\frac 1 2 \int \sqrt {1+u} \frac {1}{1-2sin^2(x)}du \\ &=\frac 1 2 \int \sqrt u \frac{1}{1-2(u-1)^2}du =\frac 1 2 \int \sqrt u \frac{1}{-2u^2+4u-1}du \\ & not work \end{aligned}$

$\begin{aligned} &\int \sqrt{1 + sin(2x)} dx \\ &u=\sqrt{1 + sin(2x)}, du=\frac{2cos(2x)}{2\sqrt{1 + sin(2x)}}dx\\ &u^2-1=sin(2x)\\ &=\int u\frac{u}{cos(2x)} du = \int \frac{u^2}{\sqrt{1-(u^2-1)^2}}du\\ & t=u^2-1, dt=2udu\\ &=\frac{1}{2} \int \frac{u}{\sqrt{1-t^2}}dt=\frac{1}{2}\int \frac{\sqrt{1+t}}{\sqrt{1-t}\sqrt{1+t}}dt \\ &=\frac{1}{2}\int \frac{1}{\sqrt{1-t}}dt=\frac{1}{2}\int (1-t)^{-1/2}dt=\frac 1 2 (2)(1-t)^{1/2}\\ &=\sqrt{1-t}=\sqrt{2-u^2}=\sqrt{2-(1+sin(2x))}\\ &=\sqrt{1-sin(2x)}+C\\ &=\sqrt{cos^2x+sin^2x-2sinxcos}+C=|cosx-sinx|+C \end{aligned}$
Alt.
$1=sin^2x+cos^2x\\ \int \sqrt{1 + sin(2x)} dx =\int \sqrt {sin^2x+cos^2x+2sinxcosx} dx\\ =\int (sinx+cosx)dx=-cosx+sinx+C$

96. $\int x^{1/4} dx$

$\begin{aligned} &\int x^{1/4} dx \\ &=\frac 4 5 x^{\frac 5 4}+C \end{aligned}$

97. $\int \frac{1}{1 + e^x}dx$

$\begin{aligned} &\int \frac{1}{1 + e^x} dx \\ & u = 1+e^x, du=e^x dx \\ &=\int \frac {1}{u} \frac{1}{u-1}du=\int \frac{-1}{u}+\frac{1}{u-1}du \\ &=-ln|u|+ln|u-1|\\ &=ln|\frac{u-1}{u}|=ln|\frac{e^x}{1+e^x}|+C\\ &=x-ln(1+e^x)+C \end{aligned}$

98. $\int \sqrt{1 + e^x} dx$

$\begin{aligned} &\int \sqrt{1 + e^x} dx \\ & u=\sqrt{1+e^x}, du=\frac{e^x}{2\sqrt{1+e^x}}dx\\ &=\int u \frac{2u}{e^x}du=2\int \frac {u^2-1+1}{u^2-1}du\\ &=2(u-\int \frac{1}{1-u^2} du)=2u-2arctanh(u)+C\\ &=2\sqrt{1+e^x}-2tanh^{-1}(\sqrt{1+e^x})+C\\ &=2\sqrt{1+e^x}-2\frac{1}{2}ln |{\frac{1+\sqrt{1+e^x}}{1-\sqrt{1+e^x}}}|+C\\ &=2\sqrt{1+e^x}+ln |{\frac{1-\sqrt{1+e^x}}{1+\sqrt{1+e^x}}}|+C\\ \end{aligned}$
$arctanh{x}=\frac{1}{2}\ln |\frac{1+x}{1-x}|$

99. $\int \frac{\sqrt{tan(x)}}{sin(2x)}dx$

$\begin{aligned} &\int \frac {\sqrt{tan(x)}}{sin(2x)}dx =\int \frac {\sqrt{tan(x)}}{2sin(x)cos(x)} dx\\ &u=\sqrt {tan(x)}, du=\frac{sec^2x}{2\sqrt{tanx}}dx \\ &=\int \frac {u}{2sinxcosx}\frac{2u}{sec^2x}du \\\\ &=\int \frac{2tan(x)cos(x)}{2sinx} du \\ &=\int du= u =\sqrt{tan(x)}+C \end{aligned}$

100. $\int_0^{\pi/2} \frac{1}{1 + sin(x)} dx$

$\begin{aligned} &\int_0^{\pi/2} \frac{1}{1 + sin(x)} dx \\ & \text{div cos} \\ &=\int \frac{secx}{secx+tanx}dx\\ & u=secx+tanx, du=(secxtanx+sec^2x )dx\\ &=\int \frac{secx}{u} \frac{1}{secx(tanx+secx)}du\\ &=\int \frac{1}{u^2}du = -\frac{1}{u}\\ &=-\frac{1}{secx+tanx}+C=-\frac{cosx}{1+sinx}+C \\ & -\frac{cosx}{1+sinx} ]_0^{\pi/2} =0-(-1)\\ &=1 \end{aligned}$
Alt.
$\begin{aligned} &\int_0^{\pi/2} \frac{1}{1 + sin(x)} dx \\ &=\int_0^{\pi/2} \frac{1-sin(x)}{1 - sin^2(x)} dx =\int \frac{1-sin(x)}{cos^2(x)} dx\\ &=\int sec^2x-sec(x)tan(x)dx=tan(x)-sec(x)+C\\ &=tan(x)-sec(x) ]_0^{\pi/2} not solve. \\ &=\frac{sin(x)-1}{cos(x)}=-\frac{cos^2(x)}{cos(x)(1+sin(x))}=-\frac{cos(x)}{1+sin(x)} \end{aligned}$

101. $\int \frac {sin(x)} x + ln(x)cos(x) dx$

$\begin{aligned} &\int \frac{sin(x)}{x} + ln(x)cos(x) dx \\ &=\int \frac{sinx}{x}dx+\int ln(x)cos(x)dx\\ &=sin(x)ln(x)- \int cos(x)ln(x)dx+\int ln(x)cos(x)dx\\ &=sin(x)ln(x)+C \end{aligned}$

Author: crazyj7@gmail.com

90. $\int_{0}^{\frac{\pi}{2}} \frac{sin(x)^3}{cos(x)^3 + sin(x)^3} dx$

try some.
$\begin{aligned} &\int_0^{\frac{\pi}{2}} \frac{sin(x)^3}{cos(x)^3 + sin(x)^3} dx\\ &cos^3x+sin^3x=(cos^2x+sin^2x)(cosx+sinx)-cosxsin^2x-cos^2xsinx\\ &=cosx+sinx-cosxsin^2x-cos^2sinx\\ &=cosx(1-sin^2x)+sinx(1-cos^2x) \\ & u = cos(x), du=-sin(x)dx\\ &=\int \frac{sinx(1-u^2)}{u^3+sinx(1-u^2)} (-\frac{1}{sinx})du\\ & u=cos^3x+sin^3x, du/dx=3cos^2x(-sinx)+3sin^2xcosx \\ &=\int \frac{sinx(1-cos^2x)}{cos^3x+sin^3x}dx \\ &=\int \frac{1}{cot^3x+1}dx \end{aligned}$
$\int \frac{sin^3x}{cos^3x+sin^3x} dx\\ (cosx+sinx)^3 = cos^3x+sin^3x+3cos^2xsinx+3cosxsin^2x\\ =cos^3x+sin^3x+3cosxsinx(cosx+sinx)\\ =\int \frac{1}{cot^3x+1}dx=\int \frac{1}{(1+cot^2)(cotx)-cotx+1}dx\\ =\int \frac{1}{csc^2xcotx-cotx+1}dx\\ =\int \frac{tan^3x}{1+tan^3x}dx (u=tan x, du=sec^2x dx)\\ =\int \frac{u^3}{1+u^3}\frac{1}{sec^2x}dx$

fail… very hard…

$\begin{aligned} &\text{Hint: tan x, x=arctan subs... }\\ &\int \frac{sin^3x}{cos^3x+sin^3x} dx \\ &=\int \frac{tan^3x}{1+tan^3x}dx, \quad (x=tan^{-1}y, dx=\frac{1}{1+y^2}dy)\\ &=\int \frac{y^3}{1+y^3}\frac{1}{1+y^2}dy \\ &=\int \frac{y^3+1-1}{(1+y^2)(1+y^3)}dy \\ &=\int \frac{1}{(1+y^2)}-\int \frac{1}{(1+y^2)(1+y^3)}dy \\ &=arctan(y)-\int \frac{ay+b}{1+y^2}+\frac{cy^2+dy+e}{1+y^3} dy\\ & a+c=0, b+d=0, c+e=0, d+a=0, b+e=1\\ &=a=-c, b=-d, c=-e, d-c=0, -c+-c=1, c=d=-b=-a, \\ &c=d=-(1/2), a=b=e=(1/2)\\ &\frac{(1/2)y+(1/2)}{1+y^2}+\frac{-(1/2)y^2+(-1/2)y+(1/2)}{1+y^3}\\ &=arctan(y)-\int \frac{(1/2)y+(1/2)}{1+y^2}+\frac{-(1/2)y^2+(-1/2)y+(1/2)}{1+y^3} dy\\ &=arctan(y)-\frac 1 2\int \frac{1+y}{1+y^2}dy+\frac 1 2 \int \frac{y^2+y-1}{1+y^3} dy\\ &\int \frac{1+y}{1+y^2}dy =\int \frac 1 {1+y^2}dy+\int \frac y {1+y^2}dy\\ &=arctan (y)+\frac 1 2 ln|1+y^2|\\ &R=\int \frac{y^2+y-1}{1+y^3}=\int \frac {y^2}{1+y^3}dy+\int \frac {y-1}{1+y^3}dy\\ &\int \frac {y^2}{1+y^3}dy=\frac 1 3 ln(1+y^3)\\ &y^3+1=(y+1)(y^2-y+1)\\ &\int \frac {y-1}{1+y^3}dy=\int \frac{ay+b}{y^2-y+1}+\frac{c}{y+1}dy\\ &a+c=0, b-c+a=0, b+c=1, a=-c, b=2c\\ &c=1/3, b=2/3, a=-1/3\\ &\int \frac {y-1}{1+y^3}dy=\int \frac{(-1/3)y+2/3}{y^2-y+1}+\frac{1/3}{y+1}dy\\ &=-\frac 1 3 \int \frac{y-2}{y^2-y+1}dy+\frac 1 3 \int \frac{1}{y+1}dy\\ &=-\frac 2 3 \int \frac{y-\frac 1 2-\frac 3 2 }{y^2-y+1}dy+\frac 1 3 ln|y+1|\\ &\int \frac{y-\frac 1 2-\frac 3 2 }{y^2-y+1}dy=\int \frac{y-\frac 1 2}{y^2-y+1}dy-\frac 3 2 \int \frac{1}{y^2-y+1}dy \\ &=\frac 1 2 ln(y^2-y+1) -\frac 3 2 \int \frac{1}{y^2-y+1}dy \\ &\int \frac{1}{y^2-y+1}dy=\int \frac {1}{tan^2x+1-tanx}sec^2xdx\\ &=\int \frac {sec^2x}{sec^2x-tanx}dx=\int \frac {\frac 1 {cos^2x}}{\frac{1-cosxsinx}{cos^2x}}dx=\int \frac 1 {1-cosxsinx}dx\\ &=\int \frac{2}{2- sin2x}dx\\ &\frac{1}{y^2-y+1}=c\frac {(ay+b)'}{1+(ay+b)^2}=\frac{ac}{a^2y^2+2aby+b^2+1}\\ &a/c=1, 2b/c=-1, (b^2+1)/ac=1, a=c=-2b\\ &(b^2+1)=(4b^2), 3b^2=1, b=\pm \frac 1 {\sqrt{3}} \\ &b=-\frac 1 {\sqrt 3}, a=c=\frac 2 {\sqrt 3}\\ &\frac{1}{y^2-y+1}=\frac 2 {\sqrt 3}\frac{\frac 2 {\sqrt 3}}{1+(\frac 2 {\sqrt 3}y-\frac 1 {\sqrt 3})^2}\\ &\int \frac{1}{y^2-y+1}dy=\frac 2 {\sqrt 3}\int \frac{\frac 2 {\sqrt 3}}{1+(\frac 2 {\sqrt 3}y-\frac 1 {\sqrt 3})^2} dy\\ &=\frac 2 {\sqrt 3}arctan(\frac 2 {\sqrt 3}y-\frac 1 {\sqrt 3})\\ & R=\int \frac{y^2+y-1}{1+y^3} dy = \frac1 3 ln(1+y^3)-\frac 2 3 ( \frac 1 2 ln(y^2-y+1)-\sqrt 3 arctan(\frac 2 {\sqrt 3} y-\frac 1 {\sqrt 3}) ) +\frac 1 3 ln(y+1)\\ &R=\frac 2 3 ln (y+1)+\frac 2 {\sqrt 3} arctan( \frac{2y-1}{\sqrt 3})\\ & \therefore Q=arctan(y)-\frac 1 2\int \frac{1+y}{1+y^2}dy+\frac 1 2 \int \frac{y^2+y-1}{1+y^3} dy \\ &=arctan(y)-\frac 1 2 ( arctan (y)+\frac 1 2 ln|1+y^2|)\\ &+\frac 1 2 ( \int \frac{y^2+y-1}{1+y^3} dy )\\ &=\frac 1 2 x-\frac 1 4 ln|1+tan^2x|+\frac 1 2 R\\ &=\frac 1 2 x-\frac 1 4 ln|1+tan^2x|+\frac{1}{3}ln|1+tanx|+\frac 1 {\sqrt 3}arctan(\frac {2tanx-1}{\sqrt 3}) \end{aligned}\\$
이렇게라도 해봤는데… 답이 안나옴…
답은 pi/4 라고 하니, 알아서 도전바람…
끈기 있게 다시 시도…

$\begin{aligned} &\int \frac{sin^3x}{cos^3x+sin^3x} dx \\ &=\int \frac{tan^3x}{1+tan^3x}dx, \quad (x=tan^{-1}y, dx=\frac{1}{1+y^2}dy)\\ &=\int \frac{y^3}{1+y^3}\frac{1}{1+y^2}dy \\ &=\int \frac{y^3}{(1+y^2)(1+y^3)}dy =\int \frac{y^3}{(1+y)(1+y^2)(1-y+y^2)}dy\\ &\frac{a}{y+1}+\frac{by+c}{y^2+1}+\frac{dy+e}{y^2-y+1}=\frac{ (a+b)y^2+(b+c)y+(a+c) }{y^3+y^2+y+1}+\frac{dy+e}{y^2-y+1}\\ &y^4( a+b +d)=0, y^3(b+c-a-b+e+d=1), y^2(a+c-b-c+a+b+e+d)=0,\\ &y(-a-c+b+c+e+d)=0, a+c+e=0\\ &a+c+e=0, -a+b+e+d=0, 2a+e+d=0, -a+c+d+e=1, a+b+d=0\\ &b+d=-a, -2a+e=0, e=2a, c=-3a, d=-4a, -a-3a-4a+2a=1\\ &a=-1/6, c=1/2, e=-1/3, d=2/3, b=-1/2\\ &Q=\int \frac{-1/6}{y+1}+\frac{(-1/2)y+(1/2)}{y^2+1}+\frac{(2/3)y+(-1/3)}{y^2-y+1} dy\\ &=-\frac 1 6 ln(y+1)- \frac 1 2 \int \frac{y-1}{y^2+1}dy+\frac 1 3 \int \frac{2y-1}{y^2-y+1} dy\\ &=-\frac 1 6 ln(y+1)- \frac 1 2 \int \frac y {y^2+1}dy +\frac 1 2 \int \frac 1 {y^2+1}dy+\frac 1 3 ln(y^2-y+1) \\ &=-\frac 1 6 ln(y+1)-\frac 1 4 ln(y^2+1)+\frac 1 2 arctan(y)+\frac 1 3 ln(y^2-y+1) \\ &\text{x= 0 to pi/2 , y=0 to inf. y=tan(x)}\\ &=\frac 1 2 x +\frac 1 {12} ( 4ln(y^2-y+1)-2ln(y+1)-3ln(y^2+1) )\\ &=\frac 1 2 x +\frac 1 {12} ln ( \frac{ (y^2-y+1)^4}{(y+1)^2(y^2+1)^3} ) \\ & (x=0, then Q=0 ) \\ & (x=\pi/2, then Q= \pi/4 , ( \lim_{y\to\infty} ln \frac{O(y^8)}{O(y^8)}=ln1=0) )\\ & \therefore Q=\frac {\pi}{4}\\ &Q=\frac 1 2 x +\frac 1 {12} ln ( \frac{ (y^2-y+1)^4} {(y+1)^2(y^2+1)^3} )\\ &=\frac 1 2 x +\frac 1 {12} ln( \frac{(1+tan^2x-tanx)^4}{(1+tanx)^2(1+tan^2x)^3})\\ &=\frac 1 2 x +\frac 1 {12} ln( \frac{(sec^2x-tanx)^4}{(1+tanx)^2(secx)^6})\\ &=\frac 1 2 x +\frac 1 {6} ln( \frac{(sec^2x-tanx)^2}{(1+tanx)(secx)^3})\\ &=\frac 1 2 x +\frac 1 {3} ln(\frac{1-cosxsinx}{cos^2x})-\frac 1 6 ln(\frac{cosx+sinx}{cos^4x})\\ &=\frac 1 2 x + \frac 1 3 ln(1-cosxsinx)-\frac 2 3ln(cosx)-\frac 1 6 ln(cosx+sinx)+\frac 2 3 ln(cosx)\\ &=\frac 1 2 x +\frac 1 3 ln(1-cosxsinx)-\frac 1 6 ln(cosx+sinx)+C\\ \end{aligned}$

https://math.stackexchange.com/questions/198083/int-frac-sin3x-sin3x-cos3x

Author: crazyj7@gmail.com

81. $\int \frac{sin(\frac{1}{x})}{x^3}dx$

$\begin{aligned} &\int \frac{sin(\frac{1}{x})}{x^3}dx \\ &(u=\frac{1}{x}, du=-x^{-2}dx)\\ &=\int sin(u)x^{-3}(-x^2)du=-\int sin(u)x^{-1}du=-\int u \sin(u)du\\ &=-( u(-cos(u))-(-sin(u)) )=ucos(u)-sin(u)\\ &= \frac{1}{x} cos( \frac{1}{x})-sin(\frac{1}{x})+C \end{aligned}$